
- Autor Stanley Ellington [email protected].
- Public 2023-12-16 00:12.
- Zuletzt bearbeitet 2025-01-22 15:50.
Logistische Regression ist das passende Rückschritt Analyse durchzuführen, wenn die abhängige Variable dichotom (binär) ist. Logistische Regression ist Gebraucht Daten zu beschreiben und die Beziehung zwischen einer abhängigen binären Variablen und einer oder mehreren nominalen, ordinalen, Intervall- oder Verhältnisstufen-unabhängigen Variablen zu erklären.
Es wird auch gefragt, wann logistische Regression eingesetzt werden sollte.
Wann zu verwenden Logistische Regression . Du sollen denke über die Verwendung nach logistische Regression wenn Ihre Y-Variable nur zwei Werte annimmt. Eine solche Variable wird als „binär“oder „dichotom“bezeichnet. „Dichotom“bedeutet im Wesentlichen zwei Kategorien wie ja/nein, defekt/nicht defekt, Erfolg/Misserfolg und so weiter.
Was versteht man unter logistischer Regression? Beschreibung. Logistische Regression ist eine statistische Methode zur Analyse eines Datensatzes, in dem es eine oder mehrere unabhängige Variablen gibt, die ein Ergebnis bestimmen. Das Ergebnis wird mit einer dichotomen Variablen gemessen (bei der es nur zwei mögliche Ergebnisse gibt).
Ebenso wird gefragt, wo wird die logistische Regression eingesetzt?
Logistische Regression ist Gebraucht in verschiedenen Bereichen, darunter maschinelles Lernen, die meisten medizinischen Bereiche und Sozialwissenschaften. Zum Beispiel der Trauma and Injury Severity Score (TRISS), der weit verbreitet ist Gebraucht um die Mortalität bei verletzten Patienten vorherzusagen, wurde ursprünglich von Boyd et al. mit logistische Regression.
Wie funktioniert eine logistische Regression?
Gaußsche Verteilung: Logistische Regression ist ein linearer Algorithmus (mit einer nichtlinearen Transformation am Ausgang). Es tut gehen von einer linearen Beziehung zwischen den Eingangsvariablen und der Ausgangsgröße aus. Datentransformationen Ihrer Eingabevariablen, die diese lineare Beziehung besser darstellen, können zu einem genaueren Modell führen.
Empfohlen:
Wozu dient die Series 63-Lizenz?

Die Serie 63 ist eine Wertpapierprüfung und -lizenz, die den Inhaber berechtigt, Aufträge für jede Art von Wertpapier in einem bestimmten Staat zu erbitten. Agenten müssen die Series 63-Lizenz zusätzlich zu einer Series 7- oder Series 6-Lizenz erwerben, um Wertpapiere zu verkaufen
Wozu dient die Zwei-Faktor-Authentifizierung?

Die Zwei-Faktor-Authentifizierung (2FA), manchmal auch als Zwei-Stufen-Verifizierung oder Zwei-Faktor-Authentifizierung bezeichnet, ist ein Sicherheitsprozess, bei dem Benutzer zwei verschiedene Authentifizierungsfaktoren angeben, um sich selbst zu verifizieren. Dieser Vorgang wird durchgeführt, um sowohl die Anmeldeinformationen des Benutzers als auch die Ressourcen, auf die der Benutzer zugreifen kann, besser zu schützen
Wozu dient die Fehlerbaumanalyse?

Dies wird auch als Top-Down-Ansatz bezeichnet. Der Hauptzweck der Fehlerbaumanalyse besteht darin, potenzielle Ursachen von Systemfehlern zu identifizieren, bevor die Fehler tatsächlich auftreten. Es kann auch verwendet werden, um die Wahrscheinlichkeit des Top-Ereignisses mit analytischen oder statistischen Methoden zu bewerten
Was ist logistische Regression beim Data Mining?
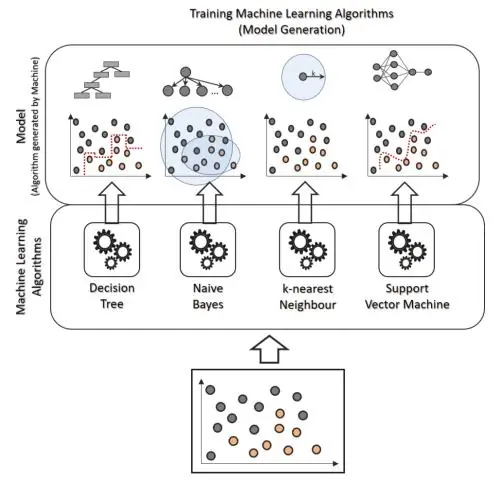
Die logistische Regression ist eine statistische Analysemethode, die verwendet wird, um einen Datenwert basierend auf früheren Beobachtungen eines Datensatzes vorherzusagen. Ein logistisches Regressionsmodell sagt eine abhängige Datenvariable vorher, indem es die Beziehung zwischen einer oder mehreren vorhandenen unabhängigen Variablen analysiert
Wozu dient die Wertberichtigung für zweifelhafte Konten?
Die Wertberichtigung für zweifelhafte Konten wird verwendet, wenn Aufwendungen für uneinbringliche Forderungen erfasst werden, bevor die spezifischen Forderungen bekannt sind, die uneinbringlich sein werden. Der Betrag des Eintrags ist der Betrag, der erforderlich ist, damit das Endguthaben auf dem Freibetragskonto ein Guthaben von 10.000 USD ist
