Video: Was ist der Unterschied zwischen einfacher und Zinseszins-Mathematik?
2024 Autor: Stanley Ellington | [email protected]. Zuletzt bearbeitet: 2023-12-16 00:12
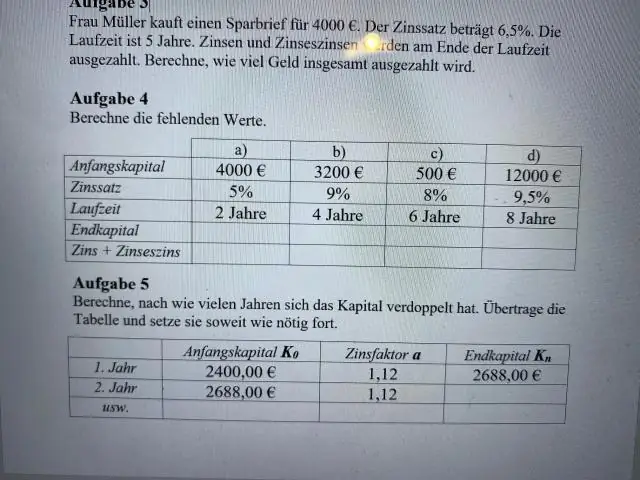
Mit einfaches Interesse die Summe von Interesse ist über einen Zeitraum fixiert von Zeit. Wichtig zu beachten mit einfaches Interesse der verdiente Betrag bleibt jedes Jahr gleich. Zinseszins . Zinseszins ist der typ von Interesse das wird normalerweise von Banken an Sparer ausgezahlt.
Was ist der Unterschied zwischen einfachen und Zinseszinsen?
Die Interesse , typischerweise in Prozent ausgedrückt, kann entweder einfach oder zusammengesetzt . Einfaches Interesse basiert auf dem Nennbetrag eines Darlehens oder einer Einlage, während Zinseszins basiert auf dem Nennbetrag und dem Interesse die sich in jeder Periode darauf ansammelt.
Was ist der Unterschied zwischen einem einfachen und einem Zinseszins-Quizlet? Einfaches Interesse ist Interesse die Zahlung wird nur auf den Hauptbetrag berechnet; wohingegen Zinseszins ist Interesse berechnet sowohl auf den Kapitalbetrag als auch auf alle zuvor angesammelten Interesse.
Wie berechnet man in diesem Zusammenhang einfache Zinsen und Zinseszinsen?
Die einfache Zinsformel ist I = P x R x T. Zinseszins berechnen mit folgendem Formel : A = P(1 + r/n) ^ nt. Angenommen, der geliehene Betrag P beträgt 10.000 US-Dollar Interesse Rate, r, ist 0,05, und die Anzahl der Male Interesse ist zusammengesetzt in einem Jahr, n, ist 4.
Was ist die beste Definition des Zinseszinses?
Zinseszins ist Interesse die auf das anfängliche Kapital und das kumulierte Interesse einer Haupteinlage, eines Darlehens oder einer Schuld. Von zusammengesetzte Zinsen , kann ein Kapitalbetrag schneller wachsen, als wenn er nur einfach kumuliert würde Interesse , das ist nur der Prozentsatz des Kapitalbetrags.
Empfohlen:
Was ist der Unterschied zwischen dem einfachen Zins- und dem Zinseszins-Quizlet?
Einfache Zinsen sind Zinsen, die nur auf den Nennbetrag berechnet werden; während der Zinseszins sowohl auf den Kapitalbetrag als auch auf alle zuvor aufgelaufenen Zinsen berechnet wird. Je höher der Zinssatz, desto schneller wächst die Einlage
Ist Zinseszins oder Zinseszins besser?
Der einfache Zins basiert auf dem Nennbetrag eines Darlehens oder einer Einlage, während der Zinseszins auf dem Nennbetrag und den darauf anfallenden Zinsen in jeder Periode basiert. Da der einfache Zins nur auf den Kapitalbetrag eines Darlehens oder einer Einlage berechnet wird, ist er einfacher zu bestimmen als der Zinseszins
Was ist der Unterschied zwischen der Gewinnspanne und der Bruttogewinnquote?
Während sie ähnliche Metriken messen, misst die Bruttomarge den Prozentsatz (oder den Dollarbetrag) des Vergleichs der Kosten eines Produkts mit seinem Verkaufspreis, während der Bruttogewinn den Prozentsatz (oder den Dollarbetrag) des Gewinns aus dem Verkauf des Produkts misst
Was ist der Unterschied zwischen der UCC-Regel für perfekte Ausschreibungen und der Common Law-Regel für nicht konforme Waren?
(UCC 2-601.) Der Käufer hat keine uneingeschränkte Möglichkeit, ein Angebot abzulehnen. Vergleichen Sie die Perfect-Tender-Regel, die nach dem Uniform Commercial Code für den Verkauf von Waren gilt, mit der Substantial-Performance-Doktrin, die im Common Law für Nicht-UCC-Fälle gilt
Was ist der Unterschied zwischen einfachen Zinsen und Zinseszinsen Warum bekommt man beim Zinseszins mehr Geld?
Während beide Arten von Zinsen Ihr Geld im Laufe der Zeit steigern werden, gibt es einen großen Unterschied zwischen den beiden. Konkret werden einfache Zinsen nur auf den Kapitalbetrag gezahlt, während der Zinseszins auf den Kapitalbetrag zuzüglich aller zuvor erwirtschafteten Zinsen gezahlt wird