Video: Wie lautet die Eulersche Formel, die die Anzahl der Flächen eines Tetraeders mit Eckpunkten als 4 und 6 Kanten verwendet?
2024 Autor: Stanley Ellington | [email protected]. Zuletzt bearbeitet: 2023-12-16 00:12
Diese Seite listet Beweise für die Euler-Formel : zum jedes konvexe Polyeder, das Nummer von Scheitelpunkte und Gesichter zusammen sind genau zwei mehr als die Nummer von Kanten . Symbolisch V−E+F=2. Zum Beispiel, a Tetraeder hat vier Ecken , vier Gesichter , und sechs Kanten ; 4 - 6 + 4 =2.
Wie groß ist die Anzahl der Flächen, wenn es 6 Scheitelpunkte und 12 Kanten gibt?
Ein Würfel oder ein Quader ist eine dreidimensionale Form mit 12 Kanten , 8 Ecken oder Scheitelpunkte , und 6 Gesichter.
Man kann sich auch fragen, wie funktioniert die Eulersche Formel? Eulersche Formel , Einer von zwei wichtigen mathematischen Sätzen von Leonhard Euler . Die erste ist eine topologische Invarianz (siehe Topologie), die sich auf die Anzahl der Flächen, Scheitelpunkte und Kanten eines beliebigen Polyeders bezieht. Es wird geschrieben F + V = E + 2, wobei F die Anzahl der Flächen, V die Anzahl der Ecken und E die Anzahl der Kanten ist.
Wie lautet die Formel für die Beziehung zwischen der Anzahl der Ecken und Kanten eines Würfels?
V - E + F = 2; oder in Worten: die Nummer von Scheitelpunkte , abzüglich der Nummer von Kanten , plus die Anzahl der Gesichter , ist gleich zu zwei.
Wie lautet die Eulersche Polyederformel?
Dieser Satz beinhaltet Die polyedrische Formel von Euler (manchmal auch genannt Eulersche Formel ). Heute würden wir dieses Ergebnis formulieren als: Die Anzahl der Ecken V, Flächen F und Kanten E in einem konvexen 3-dimensionalen Polyeder , erfüllen V + F - E = 2.
Empfohlen:
Wie lautet die Formel der Punktelastizität?
Um die Nachfrageelastizität genau zu berechnen, sollten wir die Formel für die Punktelastizität der Nachfrage (PED) verwenden: Der Absolutwert der Ableitung (dQ/dP) der nachgefragten Menge (Q) nach dem Preis (P) = 100, der wie bereits ermittelt, ist die Steigung der Nachfragefunktion (m)
Wie lautet die Formel für die Personalfluktuation?
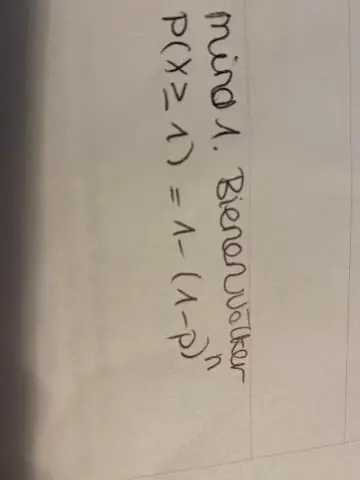
Beginnen Sie Ihre Fluktuationsberechnung, indem Sie die Gesamtzahl der Abgänge in einem Jahr durch Ihre durchschnittliche Anzahl der Mitarbeiter in einem Jahr teilen. Dann multiplizieren Sie die Zahl mit 100. Die Summe ist Ihre jährliche Fluktuationsrate in Prozent
Wie lautet die Formel für die monatliche Hypothekenzahlung?
Wenn Sie die monatliche Hypothekenzahlung von Hand berechnen möchten, benötigen Sie den monatlichen Zinssatz – teilen Sie einfach den Jahreszinssatz durch 12 (die Anzahl der Monate im Jahr). Wenn der Jahreszins beispielsweise 4 % beträgt, beträgt der monatliche Zinssatz 0,33 % (0,04/12 = 0,0033)
Wie würde sich die Anzahl der Spaltöffnungen eines Wüstenkaktus von einem Blatt unterscheiden?
Spaltöffnungen befinden sich normalerweise auf der Unterseite des Blattes. Dies hilft, den Wasserverlust zu vermeiden, indem die Stomata vor direkter Sonneneinstrahlung geschützt werden. Wie würde sich die Anzahl der Spaltöffnungen eines Wüstenkaktus von dem Blatt unterscheiden, das Sie in diesem Labor verwendet haben? Eine Wüstenpflanze hätte aufgrund der Notwendigkeit, Wasser zu sparen, weniger Spaltöffnungen
Wie lautet die Formel zur Berechnung der bereinigten Basis?
Die angepasste Basis wird berechnet, indem die ursprünglichen Kosten genommen werden, die Kosten für Verbesserungen und damit verbundene Ausgaben addiert werden und alle Abzüge für Abschreibung und Erschöpfung abgezogen werden